人工知能ブームという名のニイタカヤマをノボレ1208
おはようございますまたはこんにちはまたはこんばんは。カイヤンです。
このページをご覧いただきありがとうございます。
今回の記事は東工大ロボット技術研究会における企画、
の12月8日の記事です。あとでロ技研ブログにも転載というかリンクを張るかもしれません。
前回の記事で申し上げたことに追記する形で、今回は(タイトルは人工知能としていますが)機械学習の理論について書かせていただきたいと思います。
※このブログは数式が非常に多いです。重たいかもしれません。プレビュー機能でも処理が追い付いていない感がありました。数式の無事を祈りながら公開します。
前書き
本記事の目標は機械学習分野において広く知られている理論について、諸々の概念を東工大ロボット技術研究会という必ずしも学習系ではない学生のサークルの中でわかりやすく述べることです。この分野の詳細を述べることではありません。 また、上述しました目的のために厳密には正確でない表現となっているかもしれません。その目的の割には後半は数学的かもしれませんが、それは後述する問いかけへの回答のために、理論的であることを強調する意図があります。 従いまして、この分野について深い理解をされている方、専門家の皆さまにおかれましては、極めて自明/退屈な記事となりますことをあらかじめおわびしておきます。
本記事では機械学習の理論(学習理論)について扱います。前回申し上げた近年の人工知能「ブームを乗り越える」ということと関連する理由は、「理論的・数学的な構造を明らかにすることでホワイトボックス化し、ブームが過ぎ去ったとしてもそのあとは落ち着いた雰囲気が残るだけで閑古鳥が鳴いて分野が衰退するということは起こらないだろう。むしろ未来へ向けて発展していくだろう」と筆者が浅墓ながら考えているためです。そうして筆者は短絡的に「人工知能ブーム」を記事がアップされる予定日からの関連で「ニイタカヤマ」と結びつけています。「ブームを乗り越える」ということとニイタカヤマをノボることにかけています。
※タイトルと言えば、学習理論を「包囲」するいくつかの問いかけをABCD包囲網に喩えようとも思ったのですが、Bだけ浮かびませんでした……。Bayes統計はむしろ味方(だと思う)ですからこの世界では日英同盟だけが存続しているのかもしれません。ACDも適切かわからなかったのでいっそ書かないことにします。筆者が僭越ながら想定した3陣営だとCとDは激しく対立していますし、Aがニイタカヤマでもありません。そしてあまり本気で喩えると皆様がよくご存じなように大日本帝国が負けてしまいますし。
学習といえば次のような問いかけが散見される気がします:
「理論をやってるやつはマッドデータサイエンティストでしかないしそんなものは実際に用いるうえで必要ないのではないか」Application
「DeepLearning(深層学習,DL)により多くの構造推定や未来予知ができるようになった。DL使えばロボットだって動かせる。故に制御理論は衰退するのではないか」Connectionist
「機械学習/人工知能とりわけ神経回路網(ニューラルネットワーク、NN、含DeepLearning)は計算機の発展により計算可能になっただけの数の暴力による全くのブラックボックスであり、既存手法にとって代わりうるということは決してないし用いられるべきではない。データサイエンスなどと言うがナニカしらをやってみたばかりの理論のない分野がサイエンスを名乗るのはおこがましい。これらの分野は衰退するのではないか」Dynamics
ここではこれらへの回答もできる限りさせていただききたいと存じます。 これらは筆者の幻聴であり筆者がパラノイアになっているだけ(空集合から元をとってきている:そんなことを言う人はいない)かもしれませんが。
なお、上では人工知能は今ブームになっている(?)ような機械学習の手法によるものを指しているくらいの気持ちです。 非常に定義があいまいかつバズワードなので以下では人工知能という単語はできるだけ用いないようにします。上述しましたように、本記事が主に扱うのは機械学習についてです。それでも用いる場合はできるだけどういう意味/パラダイムの人工知能なのかを記せたらなと思います。
不良設定問題
まず機械学習の根にあると言ってもよい統計学について述べさせていただきます。先に結論を書けば、統計学は不良設定問題です。 この言い方にはいろいろな注釈が必要ですが、 注釈・詳細は以下のページを参照ということにさせてください。
このページではBayesか最尤かという問いかけが互いに深く傷つけあう以外に何もなしえず、結局正しい統計的推測というものは存在しないという認識が広まるという歴史について書かれています。†ぜったいただしいとうけいてきすいそくしゅほう†というものはありません。その意味で無料でお昼ご飯は食べられないとも言えるかもしれません。また、このとき統計学ができるのは誤差の挙動を数学的に把握することとも。数学による推論は演繹です。すなわち、数学というものそのものが間違っていることを除いて(不完全性定理まわりの話ですが勉強不足と脱線防止のため割愛)正確です。推論の誤差は正しく得られるのです。
統計学にできることは誤差の挙動を数学的に解明することです。これは統計をベースとする機械学習においても同様です。機械学習で建てられるモデルは、たとえDeepLearningであったとしてもそれはモデルに過ぎません。しかし、上のページの言葉をお借りすれば
”統計モデルや事前分布のモデリングを行うことに意味がないといっているのではありません。正しい統計モデル・正しい事前分布は存在しないということを 十分に理解した上で考察している問題に適すると考えられる統計モデルや事前分布を設計して試すことは極めて大切であり、統計モデリングとはそのような試行錯誤の手続きのことを言います。繰り返しになりますが、そのようにして試される統計モデルや事前分布は どんなに愛着があっても正しい統計モデルや正しい事前分布ではないということです”
”『真の分布がわからなくても推論の誤差を知ることができる』ところが 統計学のスゴイところです。これから統計学が発展すれば、さらに多くの普遍法則が発見されていくものと思います”
”最近よく聞かれる質問として「人工知能の推論は正しいのか」というものがあります。 今日の人工知能はデータから統計的推論を行うものですので、その正しさは統計学の正しさと 等価です。「人工知能の正しさ」を理解したい場合、統計学の本質を理解する必要があります。 統計学と同じように、人工知能は正しい推論をしませんが、しかし、その誤差については 調べることができる、ということになります” 。
モデルはモデルである。しかし数学的に推論の誤差は得られる。 そういうわけで誤差に関するさまざまな理論が研究されてきました。機械学習で用いられるモデルについてもです。機械学習による推論の誤差も理論的に解明されてきたのです。
このセクションが、すべてを神経回路網・深層学習により正しく推定できるので制御理論をはじめ他の理論は衰退するのではという問いかけや、機械学習は全くのブラックボックスであるから衰退するという問いかけへの回答になると思います。2つ目と実際に機械学習を用いる際の理論の必要性についてはより詳細を以下で述べます。
※制御理論はロボット制御に限らないものです(よね?)ので、そもそもロボットをDLで「制御」できたからといって制御理論そのものが衰退するというのも飛躍があるのですが、本記事の趣旨から外れるのでこの方向性の回答は述べないことにします。
※※詳しい人は日常的な意味の制御くらいにとらえてください。制御工学における「可制御である」という言葉の定義を確認して”「制御」できた”と書いてるわけではありません。
機械学習で用いられるモデル~特異モデル
ここから先は機械学習で用いられるモデルによる推論の誤差に対しどのような理論解明がされてきたのかを紹介させていただきます。そしてその前提としてまず機械学習でよく用いられるモデルが持つ特徴についてゆるふわに書かせていただきます。
誠に申し訳ありませんが、数式をふんだんに使わせてください。
正則モデル
定義(正則モデル)
学習モデルが以下の条件を満たすとき、統計的正則モデル或いは単に正則モデルであるという。
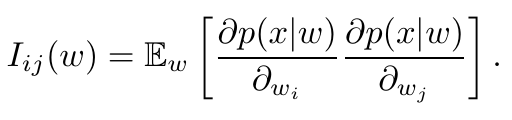
正則モデルは最尤推定量が漸近正規性を持ちます。Bayes推定においては事後確率が正規分布に漸近的に近似できることの理論保証があります。そのため非常に扱いやすいです。
この正則モデルに関して様々な理論が研究されてきました。とくに有名なものは以下で述べる事実です。そのために少々準備もさせてください。
汎化誤差
真の分布(実際にはわからない!-!!!)をとする。汎化誤差Gは次の式で定義される:
ここで
で、前者はBayes予測分布、後者は真の分布に従うn個の独立確率変数である。
この汎化誤差がいわゆる推定精度です。確率密度函数たちの距離のようなもの(正定値かつ0となるのは二つの引数が等しいときに限る)として頻繁に用いられるものにカルバックライブラ情報量がありますが、これを用いると
と書けます。なお実際にはKL情報量は距離というよりはその二乗のような性質(三角不等式は成り立たないが三平方定理のような等式が成り立つ)を持つことが知られていますが、ここでは省略します。また、物理学ではKL情報量は相対エントロピーと呼ばれます。これらは同じものです。
この汎化誤差の、データのとり方についての平均値を]と書くとすると、次のような強力な理論が知られています。
汎化誤差の平均値の漸近挙動
学習データ数をn、パラメータ空間の次元をdとするとき、次が成立する:
この漸近挙動は赤池情報量規準AICの導出及び理論保証に結びつくものです。AICの定義などは省略しますが、ここでは「真の分布がわからなくとも汎化誤差の平均値を漸近的に計算できる量」と説明させてください。
もう一つ情報量規準の紹介とその準備をさせてください。
負の対数周辺尤度or自由エネルギー
を事前分布とする。負の対数周辺尤度Fは次の式で定義される。自由エネルギーとも呼ばれる。
この量は推定精度というよりモデル選択をするにあたって非常に有用であることが知られています。事前分布を用いているようにこれはBayesの立場の量です。この量についても漸近挙動が解明されています。
自由エネルギーの漸近挙動
汎化誤差の平均値の漸近挙動及び自由エネルギーの定義と同じ仮定を置く。次が成立する:
そしてこの式はベイズ情報量規準BICの導出と理論保証に結びつきます。BICの定義も省略とさせてください。ここでは「真の分布がわからなくとも自由エネルギーを漸近的に計算できる量」とさせてください。
以上のように正則モデルについて様々な理論があります。しかしこれらはあくまで正則モデルについて成立するものです。 そして幸か不幸か、機械学習で用いられるモデルの多くは正則ではないモデル:特異モデルです。
特異モデル
特定可能・不能
ある学習モデルが特定可能であるとは、パラメータの集合から確率密度函数の集合への写像が単射でないことを言う。そうでないモデルをパラメータが特定不能であると言う。
特異点・特異モデル
Fisher情報行列が固有値0を含むようなパラメータwのこと。パラメータが特定不能ならばそのモデルは特異点を持つことが知られている。
特異点を持つようなモデルを特異モデルと言う。
特異モデルは正則でないので、最尤推定量は漸近正規性を持ちません。さらにBayes事後確率も正規分布に近似できません。そして上で述べた正則モデルの理論は使えません。パラメータ空間の次元だけで汎化誤差の平均値や自由エネルギーの漸近挙動は解明できません。AICやBICを使うことはできません。
特異点の測度は0なのだから正則理論が使えるという主張がありますが、これは間違いです。ゆるふわな説明をさせていただきますが、学習に効く点が特異点になっているのです。
では特異モデルとは非常に特殊で純粋数学的な病的なモデルなのでしょうか。そんなことはありません。 ニューラルネットワーク、混合正規分布、縮小ランク回帰、ベイジアンネットワーク、隠れマルコフモデルなどなど機械学習でよく見られるモデルは特異モデルです。階層的な構造や隠れ変数の存在が特定不能性・特異性に効いてきています。そしてこれらは近年の人工知能の制作だけでなく情報システムの構築、画像や音声などのパターン認識、遺伝子解析、テキストマイニングなどなどに用いられています。
全くのブラックボックスなモデルが上述した分野では用いられているのでしょうか。機械学習で用いられるモデルは、特異であるがゆえに正則理論が使えないということが理論的にわかっているだけなのでしょうか。そうでもありません。どれだけのことが理論解明されているのかを後述します。
特異モデルを含む一般理論
ここで一般理論はBayes推定についてです。なぜ最尤推定ではないのかを一言で述べますと、特異モデルでは最尤推定量が漸近正規性を持たないだけでなく、最尤法は汎化誤差をBayes法に比べて大きくしてしまう:最尤法はBayes法に比べ推定精度が悪いということが数学的に証明されているためです。 上でも述べたようにBayes法は正しい推測ではありませんが、最尤法よりも汎化誤差を小さくできるという意味で用います。汎化誤差を小さくできるという事実は数学の定理で、推測結果や数値実験によってのみ判明しているものではありません。
なお、正則モデルのところで述べた汎化誤差の平均値の漸近挙動などなどもBayes法による枠組みの中です。このような理論保証があることも、正則特異を問わずBayesの強力な点と言えるでしょう。
上で述べた正則モデルに関する理論は、特異モデルを含む一般のモデルではどのようになるのでしょうか。本セクションではそれを紹介いたします。 それがすなわち、特異モデルをモデルとする機械学習の手法の一般理論になるわけです。
代数幾何学と一般理論の標準形
上でも述べましたように、ここで紹介させていただく理論は一般の場合です。すなわち、事後確率が正規分布に近似できる場合もできない場合も含みます。 そのようなものをそのまま扱うのは非常に困難ですが、ここで代数幾何学の力を借り、一般理論の標準形を作ります。
誠に申し訳ございません、以下はいままで以上にゆるふわな説明になります。
学習理論やBayes推定の一般理論で用いられる形の特異点解消定理を紹介します。
特異点解消定理(広中)
を開集合
上の非負値解析函数とし、その零点集合は空でないものとする(代数幾何の意味の特異点がなくとも良い)。
このときあるd次元多様体Mと解析写像
が存在してMのチャートごとに非負整数
と正値解析函数
を用いて
一般にの零点集合は特異点を含むことがあります。しかしこの定理を用いた形
の零点集合が持つ特異点は
上の定理により
特異点解消定理と多様体の1の分割(省略します)を用いることにより、標準形に直します。
標準形への直し方ですが……紹介記事で大きく端折ることが正当かはわかりませんが、rogy AdCの記事なので端折らさせてください。 後で参考文献を挙げます。
実対数閾値と汎化誤差・自由エネルギー
特異点解消定理と1の分割の力を借りて一般理論を標準形に直すということを紹介しました。 特異点解消定理という純粋数学の定理が、応用数学たる統計学、さらに応用らしい機械学習へ応用されているわけです。 こちらでは代数幾何学のこの分野への応用、というよりも代数幾何学の構造が応用分野で出てくるというお話を紹介いたします。 そしてこのサブセクションこそ、一般理論が一般理論たる場所です。
ここまでの時点で、深淵なる数学理論が機械学習の根底にあり、そして機械学習自体も理論的なものはあるということはお察しいただけていると思いますので、機械学習は理論がない・データサイエンスに理論はないということについての回答は明らかでしょう。応用性はもう少しお待ちください。
学習理論のゼータ函数
学習理論のゼータ函数とは次で定義される1変数複素函数である:
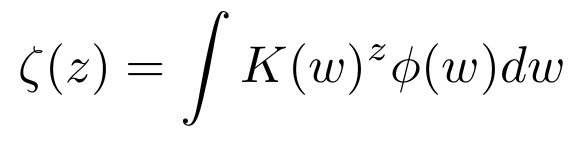
ただしである。
積分範囲はパラメータ空間全範囲ですが特異点解消定理と1の分割により
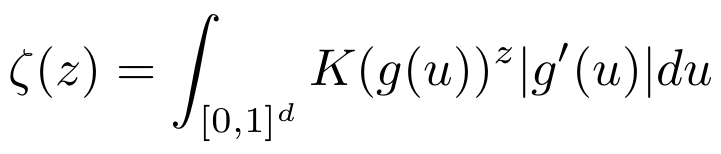
を考えます。この形にすることで、この函数が複素数平面全体に有理型函数に解析接続することができ、その極は全て負の有理数であるということが証明できます。
実対数閾値

この函数の極を考える。極に影響を与えないのでを除き、積分範囲故に絶対値を外した

を考えると
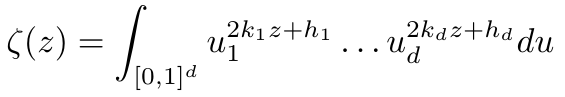
この実対数閾値が一般理論において非常に重要な役割を果たします。実はこの実対数閾値は座標のとり方・特異点解消の仕方に依存しません。 代数幾何学の言葉で双有理不変量と呼ばれる不変量です。代数幾何における不変量なのですが、次に述べさせていただきますように Bayes統計の一般理論(含機械学習)において非常に重要な現れ方をします。
一般モデルの汎化誤差の平均値の漸近挙動
学習データ数をnとするとき、次が成立する:
この漸近挙動は正則理論においてd/2をλに置き換えたものです。実際正則モデルにおいては
自由エネルギーについても同様です。
自由エネルギーの漸近挙動
汎化誤差の平均値の漸近挙動及び自由エネルギーの定義と同じ仮定を置く。次が成立する:
そしてこの式は「広く使えるベイズ情報量規準」WBICの導出と理論保証に結びつきます。これもWAICとAICの関係と同様のものが成り立ちますし、一般モデルにおいて「真の分布がわからなくとも自由エネルギーを漸近的に計算できる」のです。
申し訳ありませんが、WAIC及びWBICの定義は省略します。後で参考文献を紹介いたします。
正則と特異に関する数学的基礎や学習理論の結果の違いをまとめた表が(英語ですが)こちらのRegular and Singularにわかりやすくまとまっています。
応用と理論
「代数幾何の不変量が特異モデルで(従って機械学習で)現れるのは分かったが結局漸近挙動は未知定数λが入ってわからないじゃないか」
とお考えになるかもしれません。このままでは一般理論は構築できましたが、それぞれのモデルでどのような漸近挙動かはλを求めないとわかりません。
このλは一般に特異点解消を行うことにより計算されます。 機械学習で用いられるモデルの推定精度を調べる問題は、代数幾何学の問題に帰着されます。
3層ニューラルネットワーク、混合正規分布、ベイジアンネットワーク、隠れマルコフモデルではこのλの上界が理論的に導出されています。
縮小ランク回帰はニューラルネットワークにおけるエッジの函数をシグモイドではなくidentityにしたものですが、 こちらの実対数閾値は全ての場合において求まっています。 他にもボルツマンマシンなどいくつかの機械学習のモデルにおいて実対数閾値について解明されつつあります。 また、実対数閾値を用いてモデル選択をしてみようという論文がごく最近採択されたようです。
また、WAICやWBICの導出にはこれらの理論が必要不可欠でした。ここでは紹介しきれませんでしたが、学習の状態方程式と呼ばれる、経験誤差から汎化誤差の平均値を推定する方程式もあります。この方程式は漸近的なものではありません。 以上のように、理論は役に立つというわけです。
では実際に用いるうえで理論を知る必要があるのかというのは、若干微妙な問題です。 ここで述べたような結果は便利でしょう。しかしここで述べた結果の証明をすべて自力でフォローできなければならないという点は、推奨されても必須とまでは言えないでしょう。特に特異点解消定理の証明は代数幾何学の専門家でもない限りフォローは難しいと思われます。
しかし、理論を全く知らないと混合正規分布の計算に最尤法であるEMアルゴリズムを用いてしまったり(代わりに変分ベイズ法と呼ばれる手法が推奨されています)、特異モデルにAICやBICを用いてしまうという事故が起きます。 そのため、理論が不要である:そんなものはマッドデータサイエンティストのみが扱う、ということはないと思います。
おわりに
筆者が勉強したこと・そしてrogyで紹介したいと思ったことをつらつらと書き連ねました。まだ説明不足感はある(状態方程式、クロスヴァリデーション)のですが、これ以上数式をはてなのmdで打ち込むのがつらい&ページが重くなるのでこのへんで筆を置こうと思います。ここからは本セクションは筆者のぼやき感が強いです。
深層学習(4層以上の神経回路網)のようにまだ理論保証が未解明な手法もあるにはありますが、ブラックボックスさや解釈可能性の難しさについて実験的にでも様々な研究がされているものもあります。つまり、ほげほげという実問題に深層学習でうおーーっとニューロンを繋げに繋げてGPUパワーでうがーーっと計算して結果が出た! というのばかりがデータサイエンスというのは非常に大きな誤解です。深層学習に限らず他の手法に関してもです。
そして最初に紹介させていただきましたように、モデルはモデルに過ぎません。従って深層学習が脳の生物的な神経回路網の本当の挙動を表しているわけではありませんし、真の画像認識をできるわけでもありません。よって深層学習によりなんでもかんでも解決できるかというのは、解決の意味にもよりますが難しいと思います。例えばレベル4自動運転への応用は、現状、ブラックボックス性がおそらく法的にも非常に引っかかるでしょう。学習の結果後ろに目がついてるようなことになり、「安全」と評価関数が判断してしまえば交差点でバックをしてしまったりもするといいます。しかし深層学習が知識発見の方向性で多くの成果を出しているのもまた事実です。深層学習でなんでもかんでもやるのではなく、そのブラックボックス性と解釈の難しさとは向き合っていかなければならないでしょう。そうして適切に使われた場合、これまで誰も思いもよらなかった発見があるかもしれません。または、深層学習に変わるより理論保証のある手法が生まれるかもしれません。深層学習は有用な場面が存在しますが、任意の場面で有用ではないと思います。
よその分野を頭ごなしに衰退するなどとは、言うことはできないでしょうし言ってはならないとも思います。そちらの分野の知見がどこかで生きてくるのかもしれませんから。むしろブームを乗り越えるために異分野間で手を取り合っていければ・共存していければ良いと思います。 私にその方法はわかりませんが(制御理論と機械学習の関わりという形でシステム同定というものがあると聞いたことがあるのですが全くの勉強不足です)、 『もののけ姫』のアシタカ風に言えば「共に生きることはできる」と思います。このあとモロに言われたサンと共に戦うのかという問いに、それでは憎しみを生むだけだとアシタカは答えていますが、勉強不足ながらも今の状況はなんとなくかつての最尤VSベイズを彷彿とさせます。つまり存在しない「正しい推測手法」を 求め、互いに憎しみを生みあい、深く傷つけ合って終わった†論争†を思い起こさせるのです。
この記事は機械学習の理論をわかりやすく紹介する記事でした。知っている人には「それはそう」という話ばかりだったと思いますし、これだけでブームを 乗り越えられるのかと言うとそんなことはないと思います。 もっと数学的な記事を期待した方は数式表示のことも含めてがっかりされたかもしれません(参考文献や原著論文をフォローしていただければご満足いただけるかもしれません)。 筆者がブームを乗り越えるにはと浅墓に考えた「理論的・数学的な構造を明らかにすることでホワイトボックス化し、ブームが過ぎ去ったとしてもそのあとは落ち着いた雰囲気が残るだけで閑古鳥が鳴いて分野が衰退するということは起こらないだろう。むしろ未来へ向けて発展していくだろう」という気持ちを原動力に、そして機械学習の理論に対する誤解(実務に理論は不要、深層学習は万能、データサイエンスに理論はない)を少しでも解消できたらなという気持ちを抱いて書きました。最後まで付き合っていただき誠にありがとうございました。
参考文献
この記事のかなりの部分はこの2冊を参考・引用させていただいたものです。前者の英語版は日本語版に比べ行間が少なく、 著者のページでも専門書ではなく入門書とされているようです。
また上2冊の著者である渡辺澄夫先生のWebページ(上述リンク)もかなり参考にさせていただきました。 本記事で定義を省略した諸々ですが、上の本の他に渡辺先生の次のページに書いてあります。特にWBICについては2冊目にも採録が間に合わなかったようです(本でないかなあ)。
本記事序盤にもリンクがあり引用させていただいておりますが、誤解を解きたいという気持ちを記事にするにあたって
を書き方という方向性でも参考にさせていただいた部分があります。 『千と千尋の神隠し』に代わり『もののけ姫』を引用している箇所は完全に触発されています。
それでは、本当にこれでおしまいです。ありがとうございました。
追記
WBICだけでなく、singular BIC(sBIC)が新たに開発されたようです。上述した実対数閾値をモデル選択に用いることを提案しているようですが、まだしっかりと読めていません。